Grandma’s Cookies (and Pure Functions)

To help explain why pure functions are important, I’d like to share a little story …

Once upon a time I was a freshman in college, and my girlfriend’s grandmother sent her a tin full of cookies. I don’t remember if there were different kinds of cookies in the package or not — all I remember is the chocolate chip cookies. Whatever her grandmother did to make those cookies, the dough was somehow more white than any other chocolate chip cookie I had ever seen before. They also tasted terrific, and I ate most of them. (Sorry about that.)

Some time after this, my girlfriend — who would later become my wife — asked her grandmother how she made the chocolate chip cookies. Grandmother replied, “I just mix together some flour, butter, eggs, sugar, and chocolate chips, shape the dough into little cookies, and bake them at 350 degrees for 10 minutes.” (There were a few more ingredients, but I don’t remember them all.)

Later that day, my girlfriend and I tried to make a batch of cookies according to her grandmother’s instructions, but no matter how hard we tried, they always turned out like normal cookies. Somehow we were missing something.

Perplexed by this mystery — and hungry for a great cookie — I snuck into grandmother’s recipe box late one night. Looking under “Chocolate Chip Cookies,” I found these comments:

/**
 * Mix together some flour, butter, eggs, sugar,
 * and chocolate chips. Shape the dough into 
 * little cookies, and bake them at 350 degrees
 * for 10 minutes.
 */

“Huh,” I thought, “that’s just what she told us.”

I started to give up on my quest after reading the comments, but the desire for a great cookie spurred me on. After thinking about it for a few moments, I realized that I could decompile grandmother’s makeCookies recipe to see what it showed. When I did that, this is what I found:

def makeCookies(ingredients: List[Ingredient]): Batch[Cookie] = {
    val cookieDough = mix(ingredients)
    val betterCookieDough = combine(cookieDough, love)
    val cookies = shapeIntoLittleCookies(betterCookieDough)
    bake(cookies, 350.DegreesFahrenheit, 10.Minutes)
}

“Aha,” I thought, “here’s some code I can dig into.”

Looking at the first line, the function declaration seems fine:

def makeCookies(ingredients: List[Ingredient]): Batch[Cookie] = {

Whatever makeCookies does, as long as it’s a pure function — where its output depends only on its declared inputs — its signature states that it transforms a list of ingredients into a batch of cookies. Sounds good to me.

The first line inside the function says that mix is some sort of algorithm that transforms ingredients into cookieDough:

val cookieDough = mix(ingredients)

Assuming that mix is a pure function, this looks good.

The next line looks okay:

val betterCookieDough = combine(cookieDough, love)

Whoa. Hold on just a minute … now I’m confused. What is love? Where does love come from?

Looking back at the function signature:

def makeCookies(ingredients: List[Ingredient]): Batch[Cookie] = {

clearly love is not defined as a function input parameter. Somehow love snuck into this function. That’s when it hit me:

Taking a deep breath to get control of myself, I looked at the last two lines of the function, and with the now-major assumption that shapeIntoLittleCookies and bake are pure functions, those lines look fine:

val cookies = shapeIntoLittleCookies(betterCookieDough)
bake(cookies, 350.DegreesFahrenheit, 10.Minutes)

“I don’t know where love comes from,” I thought, “but clearly, it is a problem.”

In regards to the makeCookies function, you’ll hear functional programmers say a couple of things about love:

• love is a hidden input to the function

• love is a “free variable”

These statements essentially mean the same thing, so I prefer the first statement: to think of love as being a hidden input into the function. It wasn’t passed in as a function input parameter, it came from … well … it came from somewhere else … the ether.

Imagine that makeCookies is the only function you have to write today — this function is your entire scope for today. When you do that, it feels like someone teleported love right into the middle of your workspace. There you were, minding your own business, writing a function whose output depends only on its inputs, and then — Bam! — love is thrown right into the middle of your work.

Put another way, if makeCookies is the entire scope of what you should be thinking about right now, using love feels like you just accessed a global variable, doesn’t it?

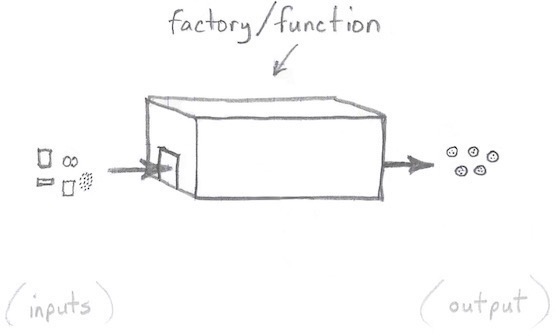
With pure functions I like to think of input parameters as coming into a function’s front door, and its results going out its back door, just like a black box, or a factory, as shown in Figure [fig:cookieFactory].

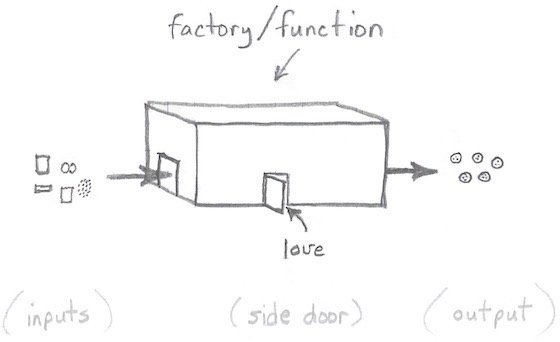
But in the case of makeCookies it’s as though love snuck in through a side door, as shown in Figure [fig:cookieFactorySideDoor].

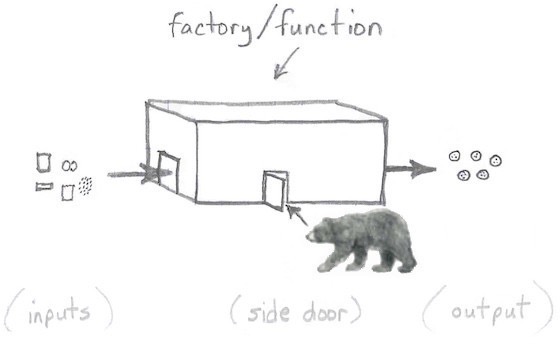
While you might think it’s okay for things like love to slip in a side door, if you spend any time in Alaska you’ll learn not to leave your doors open, because you never know what might walk in, as shown in Figure [fig:cookieFactorySideDoorBear].

When I wrote about hidden inputs I also mentioned the term “free variable,” so let’s look at its meaning. Ward Cunningham’s c2.com website defines a free variable like this:

“A free variable is a variable used within a function, which is neither a formal parameter to the function nor defined in the function’s body.”

That sounds exactly like something you just heard, right? As a result, I prefer to use the less formal term, “hidden input.”

If Scala required us to mark impure functions with an impure annotation, makeCookies would be declared like this as a warning to all readers that, “Output depends on something other than input”:

@impure
def makeCookies ...

And because makeCookies is an impure function, a good question to ask right now is:

The answer is that because love comes into the function through a side door, it can change the makeCookies result without you ever knowing why you can get different results when you call it. (Or why my cookies never turn out right.)

I like to “speak in source code” as much as possible, and a little code right now can show what a significant problem hidden inputs are, such as when you write a unit test for an impure method like makeCookies.

If you’re asked to write a ScalaTest unit test for makeCookies, you might write some code like this:

test("make a batch of chocolate chip cookies") {
    val ingredients = List(
        Flour(3.Cups),
        Butter(1.Cup),
        Egg(2),
        Sugar(1.Cup),
        ChocolateChip(2.Cups)
    )
    val batchOfCookies = GrandmasRecipes.makeCookies(ingredients)
    assert(cookies.count == 12)
    assert(cookies.taste == Taste.JustLikeGrandmasCookies)
    assert(cookies.doughColor == Color.WhiterThanOtherCookies)
}

If you ran this test once it might work fine, you might get the expected results. But if you run it several times, you might get different results each time.

That’s a big problem with makeCookies using love as a hidden input: when you’re writing black-box testing code, you have no idea that makeCookies has a hidden dependency on love. All you’ll know is that sometimes the test succeeds, and other times it fails.

Put a little more technically:

• love’s state affects the result of makeCookies

• As a black-box consumer of this function, there’s no way for you to know that love affects makeCookies by looking at its method signature

If you have the source code for makeCookies and can perform white-box testing, you can find out that love affects its result, but that’s a big thing about functional programming: you never have to look at the source code of a pure function to see if it has hidden inputs or hidden outputs.

I’ve referred to hidden inputs quite a bit so far, but hidden outputs — mutating hidden variables or writing output — are also a problem of impure functions.

However, now that I do have the makeCookies source code, several questions come to mind:

• Does love have a default value?

• How is love set before you call makeCookies?

• What happens if love is not set?

Questions like these are problems of impure functions in general, and hidden inputs in particular. Fortunately you don’t have to worry about these problems when you write pure functions.

When you write parallel/concurrent applications, the problem of hidden inputs becomes even worse. Imagine how hard it would be to solve the problem if love is set on a separate thread.

Every good story should have a moral, and I hope you see what a problem this is. In my case, I still don’t know how to make cookies like my wife’s grandmother did. (I lay in bed at night wondering, what is love? Where does love come from?)

In terms of writing rock-solid code, the moral is:

• love is a hidden input to makeCookies

• makeCookies output does not depend solely on its declared inputs

• You may get a different result every time you call makeCookies with the same inputs

• You can’t just read the makeCookies signature to know its dependencies

Programmers also say that makeCookies depends on the state of love. Furthermore, with this coding style it’s also likely that love is a mutable var.

My apologies to my wife’s grandmother for using her in this example. She was the most organized person I ever met, and I’m sure that if she was a programmer, she would have written pure functions. And her cookies are sorely missed.

Given all of this talk about pure functions, the next lesson answers the important question, “What are the benefits of pure functions?”

• The Wikipedia definition of a pure function

• Wikipedia has a good discussion on “pure functions” on their Functional Programming page

• My unit test was written using ScalaTest.

• When you need to use specific quantities in Scala applications, Squants offers a DSL similar to what I showed in these examples.