Recursion: Let’s Look at Lists

Because the List data structure — and the head and tail components of a List — are so important to recursion, it helps to visualize what a list and its head and tail components look like. Figure [fig:headTailWorm] shows one way to visualize a List.

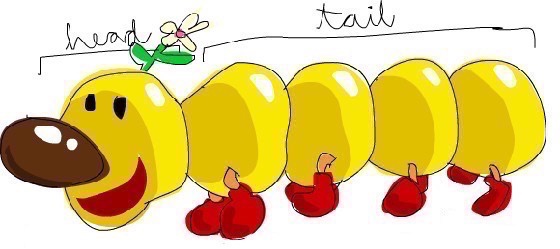
This creative imagery comes from the online version of “Learn You a Haskell for Great Good”, and it does a great job of imprinting the concept of head and tail components of a list into your brain. As shown, the “head” component is simply the first element in the list, and the “tail” is the rest of the list.

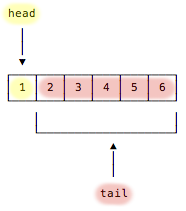
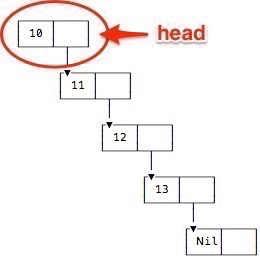
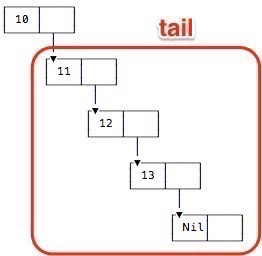
A slightly more technical way to visualize the head and tail of a list is shown in Figure [fig:visualizeListMoreTech].

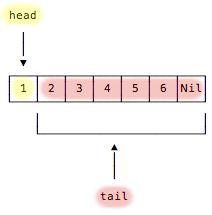
An even more accurate way to show this is with a Nil value at the end of the List, as shown in Figure [fig:visualizeListNilElement], because that’s what it really looks like:

To be clear, the List that I’m talking about is a linked list — scala.collection.immutable.List, which is the default list you get if you type List in your IDE or the REPL. This List is a series of cells, where each cell contains two things: (a) a value, and (b) a pointer to the next cell. This is shown in Figure [fig:linkedListDepiction].

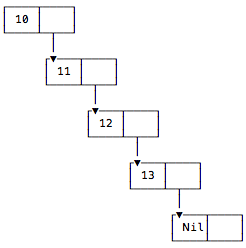
As shown, the last cell in a linked list contains the Nil value. The Nil in the last cell is very important: it’s how your recursive Scala code will know when it has reached the end of a List.

When drawing a list like this, Figure [fig:headElemOfAList] clearly shows the head element of a list, and Figure [fig:tailElemsOfAList] shows the tail elements.

Just like Haskell — and Lisp before it — the default Scala List works with these head and tail components, and I’ll use them extensively in the examples that follow.

For historical reasons these cells are known as “cons cells.” That name comes from Lisp, and if you like history, you can read more about it on Wikipedia.

As a first note about Lists, a List with no elements in it is an empty list. An empty List contains only one cell, and that cell contains a Nil element, as shown in Figure [fig:theNilList].

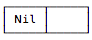
You can create an empty List in Scala in two ways:

scala> val empty = List()
empty: List[Nothing] = List()

scala> val empty = Nil
empty: scala.collection.immutable.Nil.type = List()

Because I haven’t given those lists a data type (like Int), the results look a little different, but if I add a type to those expressions, you’ll see that the result is exactly the same:

scala> val empty1: List[Int] = List()
empty: List[Int] = List()

scala> val empty2: List[Int] = Nil
empty: List[Int] = List()

scala> empty1 == empty2
res0: Boolean = true

In summary:

List() == Nil

There are several ways to create non-empty Lists in Scala, but for the most part I’ll use two approaches. First, here’s a technique you’re probably already familiar with:

val list = List(1,2,3)

Second, this is an approach you may not have seen yet:

val list = 1 :: 2 :: 3 :: Nil

These two techniques result in the exact same List[Int], which you can see in the REPL:

scala> val list1 = List(1,2,3)
list: List[Int] = List(1, 2, 3)

scala> val list2 = 1 :: 2 :: 3 :: Nil
list: List[Int] = List(1, 2, 3)

scala> list1 == list2
res1: Boolean = true

The second approach is known as using “cons cells.” As you can see, it’s a very literal approach to creating a List, where you specify each element in the List, including the Nil element, which must be in the last position. If you forget the Nil element at the end, the Scala compiler will bark at you:

scala> val list = 1 :: 2 :: 3
<console>:10: error: value :: is not a member of Int
       val list = 1 :: 2 :: 3
                         ^

I show this because it’s important — very important — to know that the last element in a List must be the Nil element. (I like to say that the Nil element is to a List as a caboose is to a train.) We’re going to take advantage of this knowledge as we write our first recursive function.