JVM Stacks and Stack Frames

For functions without deep levels of recursion, there’s nothing wrong with the algorithms shown in the previous lessons. I use this simple, basic form of recursion when I know that I’m working with limited data sets. But in applications where you don’t know how much data you might be processing, it’s important that your recursive algorithms are tail-recursive, otherwise you’ll get a nasty StackOverflowError.

For instance, if you run the sum function from the previous lessons with a larger list, like this:

object RecursiveSum extends App {

    def sum(list: List[Int]): Int = list match {
        case Nil => 0
        case x :: xs => x + sum(xs)
    }

    val list = List.range(1, 10000)  // MUCH MORE DATA
    val x = sum(list)
    println(x)

}

you’ll get a StackOverflowError, which is really counter to our desire to write great, bulletproof, functional programs.

The actual number of integers in a list needed to produce a StackOverflowError with this function will depend on the java command-line settings you use, but the last time I checked the default Java stack size it was 1,024 kb — yes, 1,024 kilobytes — just over one million bytes. That’s not much RAM to work with. I write more about this at the end of this lesson, including how to change the default stack size with the java command’s -Xss parameter.

I’ll cover tail recursion in the next lesson, but in this lesson I want to discuss the JVM stack and stack frames. If you’re not already familiar with these concepts, this discussion will help you understand what’s happening here. It can also help you debug “stack traces” in general.

If you’re already comfortable with the JVM stack and stack frames, feel free to skip on to the next lesson.

To understand the potential “stack overflow” problem of recursive algorithms, you need to understand what happens when you write recursive algorithms.

The first thing to know is that in all computer programming languages there is this thing called “the stack,” also known as the “call stack.”

Oracle provides the following description of the stack and stack frames as they relate to the JVM:

“Each JVM thread has a private Java virtual machine stack, created at the same time as the thread. A JVM stack stores frames, also called “stack frames”. A JVM stack is analogous to the stack of a conventional language such as C — it holds local variables and partial results, and plays a part in method invocation and return.”

Therefore, you can visualize that a single stack has a pile of stack frames that look like Figure [fig:aSingleStack].

As that quote mentions, each thread has its own stack, so in a multi-threaded application there are multiple stacks, and each stack has its own stack of frames, as shown in Figure [fig:multipleStacks].

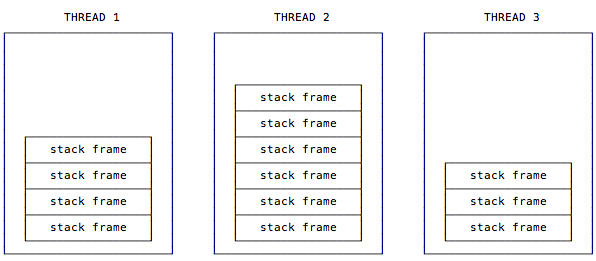
To explain the stack a little more, all of the following quoted text comes from the free, online version of a book titled, Inside the Java Virtual Machine, by Bill Venners. (I edited the text slightly to include only the portions relevant to stacks and stack frames.)

“When a new thread is launched, the JVM creates a new stack for the thread. A Java stack stores a thread’s state in discrete frames. The JVM only performs two operations directly on Java stacks: it pushes and pops frames.”

“The method that is currently being executed by a thread is the thread’s current method. The stack frame for the current method is the current frame. The class in which the current method is defined is called the current class, and the current class’s constant pool is the current constant pool. As it executes a method, the JVM keeps track of the current class and current constant pool. When the JVM encounters instructions that operate on data stored in the stack frame, it performs those operations on the current frame.”

“When a thread invokes a Java method, the JVM creates and pushes a new frame onto the thread’s stack. This new frame then becomes the current frame. As the method executes, it uses the frame to store parameters, local variables, intermediate computations, and other data.”

As the previous paragraph implies, each instance of a method has its own stack frame. Therefore, when you see the term “stack frame,” you can think, “all of the stuff a method instance needs.”

The same chapter in that book describes the “stack frame” as follows:

“The stack frame has three parts: local variables, operand stack, and frame data.”

You can visualize that as shown in Figure [fig:stackFrameDetails].

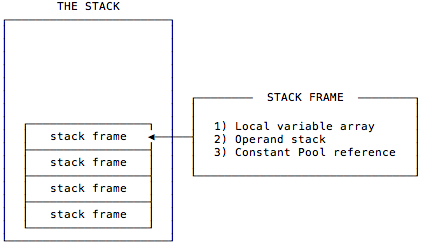
The book continues:

“The sizes of the local variables and operand stack, which are measured in words, depend upon the needs of each individual method. These sizes are determined at compile time and included in the class file data for each method.”

That’s important: the size of a stack frame varies depending on the local variables and operand stack. The book describes that size like this:

“When the JVM invokes a method, it checks the class data to determine the number of words required by the method in the local variables and operand stack. It creates a stack frame of the proper size for the method and pushes it onto the stack.”

These descriptions introduce the phrases word size, operand stack, and constant pool. Here are definitions of those terms:

First, word size is a unit of measure. From Chapter 5 of the same book, the word size can vary in JVM implementations, but it must be at least 32 bits so it can hold a value of type long or double.

Next, the operand stack is defined here on oracle.com, but as a word of warning, that definition gets into machine code very quickly. For instance, it shows how two integers are added together with the iadd instruction. You are welcome to dig into those details, but for our purposes, a simple way to think about the operand stack is that it’s memory (RAM) that is used as a working area inside a stack frame.

The Java Run-Time Constant Pool is defined at this oracle.com page, which states, “A run-time constant pool … contains several kinds of constants, ranging from numeric literals known at compile-time, to method and field references that must be resolved at run-time. The run-time constant pool serves a function similar to that of a symbol table for a conventional programming language, although it contains a wider range of data than a typical symbol table.”

I can summarize what we’ve learned about stacks and stack frames like this:

• Each JVM thread has a private stack, created at the same time as the thread.

• A stack stores frames, also called “stack frames.”

• A stack frame is created every time a new method is called.

We can also say this about what happens when a Java/Scala/JVM method is invoked:

• When a method is invoked, a new stack frame is created to contain information about that method.

• Stack frames can have different sizes, depending on the method’s parameters, local variables, and algorithm.

• As the method is executed, the code can only access the values in the current stack frame, which you can visualize as being the top-most stack frame.

As it relates to recursion, that last point is important. As a function like our sum function works on a list, such as List(1,2,3), information about that instance of sum is in the top-most stack frame, and that instance of sum can’t see the data of other instances of the sum function. This is how what appears to be a single, local variable — like the values head and tail inside of sum — can seemingly have many different values at the same time.

Not to belabor the point, but I want to share one last description of the stack (and the heap) that has specific comments about recursion. The discussion in Figure [fig:seriousStackSpace] comes from a book named Algorithms, by Sedgewick and Wayne.

There are two important lines in this description that relate to recursive algorithms:

• “When the method returns, that information is popped off the stack, so the program can resume execution just after the point where it called the method.”

• “recursive algorithms can sometimes create extremely deep call stacks and exhaust the stack space.”

From all of these discussions I hope you can see the potential problem of recursive algorithms:

• When a recursive function calls itself, information for the new instance of the function is pushed onto the stack.

• Each time the function calls itself, another copy of the function information is pushed onto the stack. Because of this, a new stack frame is needed for each level in the recursion.

• As a result, more and more memory that is allocated to the stack is consumed as the function recurses. If the sum function calls itself a million times, a million stack frames are created.