How to Write Scala Functions That Take Functions as Input Parameters
The topic I’m about to cover is a big part of functional programming: power programming that’s made possible by passing functions to other functions to get work done.
So far I’ve shown I’ve shown how to be the consumer of functions that take other functions as input parameters, that is, the consumer of Higher Order Functions (HOFs) like map and filter. In this lesson I’m going to show everything you need to know to be the producer of HOFs, i.e., the writer of HOF APIs.
Therefore, the primary goal of this lesson is to show how to write functions that take other functions as input parameters. I’ll show:
The syntax you use to define function input parameters
Many examples of that syntax
How to execute a function once you have a reference to it
As a beneficial side effect of this lesson, you’ll be able to read the source code and Scaladoc for other HOFs, and you’ll be able to understand the function signatures they’re looking for.
Before we start, here are a few notes about the terminology I’ll use in this lesson.
I use the acronym “FIP” to stand for “function input parameter.” This isn’t an industry standard, but because I use the term so often, I think the acronym makes the text easier to read.
As shown already, I’ll use “HOF” to refer to “Higher Order Function.”
As shown in the previous lessons you can create functions as variables, and because of Eta Expansion you can do that by writing them as either (a)
valfunctions or (b)defmethods. Because of this, and because I thinkdefmethods are easier to read, from now on I’ll writedefmethods and refer to them as “functions,” even though that terminology isn’t 100% accurate.
I finished the previous lesson by showing a few function definitions like this:
def isEven(i: Int) = i % 2 == 0
def sum(a: Int, b: Int) = a + b
I also showed that isEven works great when you pass it into the List class filter method:
scala> val list = List.range(0, 10)
list: List[Int] = List(0, 1, 2, 3, 4, 5, 6, 7, 8, 9)
scala> val evens = list.filter(isEven)
evens: List[Int] = List(0, 2, 4, 6, 8)
The key points of this are:
The
filtermethod accepts a function as an input parameter.The functions you pass into
filtermust match the type signature thatfilterexpects — in this case creating a function likeisEventhat takes anIntas an input parameter and returns aBoolean.
The Scaladoc shows the type of functions filter accepts, which you can see in Figure [fig:scaladocFunctionsFilterAccepts].

The Scaladoc text shows that filter takes a predicate, which is just a function that returns a Boolean value.
This part of the Scaladoc:
p: (A) => Boolean
means that filter takes a function input parameter which it names p, and p must transform a generic input A to a resulting Boolean value. In my example, where list has the type List[Int], you can replace the generic type A with Int, and read that signature like this:
p: (Int) => Boolean
Because isEven has this type — it transforms an input Int into a resulting Boolean — it can be used with filter.
The filter example shows that with HOFs you can accomplish a lot of work with a little bit of code. If List didn’t have the filter method, you’d have to write a custom method like this to do the same work:
// what you'd have to do if `filter` didn't exist
def getEvens(list: List[Int]): List[Int] = {
val tmpArray = ArrayBuffer[Int]()
for (elem <- list) {
if (elem % 2 == 0) tmpArray += elem
}
tmpArray.toList
}
val result = getEvens(list)
Compare all of that imperative code to this equivalent functional code:
val result = list.filter(_ % 2 == 0)
As you can see, this is a great advantage of functional programming. The code is much more concise, and it’s also easier to comprehend.
As FP developers like to say, you don’t tell the computer specifically “how” to do something — you don’t specify the nitty-gritty details. Instead, in your FP code you express a thought like, “I want to create a filtered version of this list with this little algorithm.” When you do that, and you have good FP language to work with, you write your code at a much higher programming level.
In many situations Scala/FP code can be easier to understand than imperative code. That’s because a great benefit of Scala/FP is that methods like filter, map, head, tail, etc., are all standard, built-in functions, so once you learn them you don’t have to write custom for loops any more. As an added benefit, you also don’t have to read other developers’ custom for loops.
I feel like I say this a lot, but we humans can only keep so much in our brains at one time. Concise, readable code is simpler for your brain and better for your productivity.
I know, I know, when you first come to Scala, all of these methods on the collections classes don’t feel like a benefit, they feel overwhelming. But once you realize that almost every for loop you’ve ever written falls into neat categories like map, filter, reduce, etc., you also realize what a great benefit these methods are. (And you’ll reduce the amount of custom for loops you write by at least 90%.)
Here’s what Martin Odersky wrote about this in his book, Programming in Scala:
“You can use functions within your code to factor out common control patterns, and you can take advantage of higher-order functions in the Scala library to reuse control patterns that are common across all programmers’ code.”
Given this background and these advantages, let’s see how to write functions that take other functions as input parameters.
To define a function that takes another function as an input parameter, all you have to do is define the signature of the function you want to accept.
To demonstrate this, I’ll define a function named sayHello that takes a function as an input parameter. I’ll name the input parameter callback, and also say that callback must have no input parameters and must return nothing. This is the Scala syntax to make this happen:
def sayHello(callback: () => Unit) {
callback()
}
In this code, callback is an input parameter, and more specifically it is a function input parameter (or FIP). Notice how it’s defined with this syntax:
callback: () => Unit
Here’s how this works:
callbackis the name I give to the input parameter. In this casecallbackis a function I want to accept.The
callbacksignature specifies the type of function I want to accept.The
()portion ofcallback’s signature (on the left side of the=>symbol) states that it takes no input parameters.The
Unitportion of the signature (on the right side of the=>symbol) indicates that thecallbackfunction should return nothing.When
sayHellois called, its function body is executed, and thecallback()line inside the body invokes the function that is passed in.
Figure [fig:howSayHelloAndCallbackWork] reiterates those points.

Now that I’ve defined sayHello, I’ll create a function to match callback’s signature so I can test it. The following function takes no input parameters and returns nothing, so it matches callback’s type signature:
def helloAl(): Unit = { println("Hello, Al") }
Because the signatures match, I can pass helloAl into sayHello, like this:
sayHello(helloAl)
The REPL demonstrates how all of this works:
scala> def sayHello(callback:() => Unit) {
| callback()
| }
sayHello: (callback: () => Unit)Unit
scala> def helloAl(): Unit = { println("Hello, Al") }
helloAl: ()Unit
scala> sayHello(helloAl)
Hello, Al
If you’ve never done this before, congratulations. You just defined a function named sayHello that takes another function as an input parameter, and then invokes that function when it’s called.
It’s important to know that the beauty of this approach is not that sayHello can take one function as an input parameter; the beauty is that it can take any function that matches callback’s signature. For instance, because this next function takes no input parameters and returns nothing, it also works with sayHello:
def holaLorenzo(): Unit = { println("Hola, Lorenzo") }
Here it is in the REPL:
scala> sayHello(holaLorenzo)
Hola, Lorenzo
This is a good start. Let’s build on it by defining functions that can take more complicated functions as input parameters.
I defined sayHello like this:
def sayHello(callback: () => Unit)
Inside of that, the callback function signature looks like this:
callback: () => Unit
I can explain this syntax by showing a couple of examples. Imagine that we’re defining a new version of callback, and this new version takes a String and returns an Int. That signature would look like this:
callback: (String) => Int
Next, imagine that you want to create a different version of callback, and this one should take two Int parameters and return an Int. Its signature would look like this:
callback: (Int, Int) => Int
As you can infer from these examples, the general syntax for defining function input parameter type signatures is:
variableName: (parameterTypes ...) => returnType
With sayHello, this is how the values line up:
| General | sayHello |
Notes |
|---|---|---|
| variableName | callback |
The name you give the FIP |
| parameterTypes | () | The FIP takes no input parameters |
| returnType | Unit |
The FIP returns nothing |
I find that the parameter name callback is good when you first start writing HOFs. Of course you can name it anything you want, and other interesting names at first are aFunction, theFunction, theExpectedFunction, or maybe even fip. But, from now on, I’ll make this name shorter and generally refer to the FIPs in my examples as just f, like this:
sayHello(f: () => Unit)
foo(f:(String) => Int)
bar(f:(Int, Int) => Int)
Using this as a starting point, let’s look at signatures for some more FIPs so you can see the differences. To get started, here are two signatures that define a FIP that takes a String and returns an Int:
sampleFunction(f: (String) => Int)
sampleFunction(f: String => Int)
The second line shows that when you define a function that takes only one input parameter, you can leave off the parentheses.
Next, here’s the signature for a function that takes two Int parameters and returns an Int:
sampleFunction(f: (Int, Int) => Int)
Can you imagine what sort of function matches that signature?
(A brief pause here so you can think about that.)
Any function that takes two Int input parameters and returns an Int matches that signature, so functions like these all fit:
def sum(a: Int, b: Int): Int = a + b
def product(a: Int, b: Int): Int = a * b
def subtract(a: Int, b: Int): Int = a - b
You can see how sum matches up with the FIP signature in Figure [fig:howSumMatchesUpFipSig].
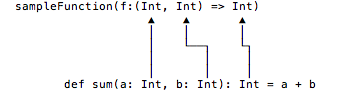
For me, an important part of this is that no matter how complicated the type signatures get, they always follow the same general syntax I showed earlier:
variableName: (parameterTypes ...) => returnType
For example, all of these FIP signatures follow the same pattern:
f: () => Unit
f: String => Int
f: (String) => Int
f: (Int, Int) => Int
f: (Person) => String
f: (Person) => (String, String)
f: (String, Int, Double) => Seq[String]
f: List[Person] => Person
I’m being a little loose with my verbiage here, so let me tighten it up for a moment. When I say that this is a “type signature”:
f: String => Int
that isn’t 100% accurate. The type signature is really just this part:
String => Int
Therefore, being 100% accurate, these are the type signatures I just showed:
() => Unit
String => Int
(String) => Int
(Int, Int) => Int
(Person) => String
(Person) => (String, String)
(String, Int, Double) => Seq[String]
List[Person] => Person
This may seem like a picky point, but because FP developers talk about type signatures all the time, I want to take that moment to be more precise.
It’s common in FP to think about types a lot in your code. You might say that you “think in types.”
Recapping for a moment, I showed the sayHello function, whose callback parameter states that it takes no input parameters and returns nothing:
sayHello(callback: () => Unit)
I refer to callback as a FIP, which stands for “function input parameter.”
Now let’s look at a few more FIPs, with each example building on the one before it.
First, here’s a function named runAFunction that defines a FIP whose signature states that it takes an Int and returns nothing:
def runAFunction(f: Int => Unit): Unit = {
f(42)
}
The body says, “Whatever function you give to me, I’m going to pass the Int value 42 into it.” That’s not terribly useful or functional, but it’s a start.
Next, let’s define a function that matches f’s type signature. The following printAnInt function takes an Int parameter and returns nothing, so it matches:
def printAnInt (i: Int): Unit = { println(i+1) }
Now you can pass printAnInt into runAFunction:
runAFunction(printAnInt)
Because printAnInt is invoked inside runAFunction with the value 42, this prints 43. Here’s what it all looks like in the REPL:
scala> def runAFunction(f: Int => Unit): Unit = {
| f(42)
| }
runAFunction: (f: Int => Unit)Unit
scala> def printAnInt (i: Int): Unit = { println(i+1) }
printAnInt: (i: Int)Unit
scala> runAFunction(printAnInt)
43
Here’s a second function that takes an Int and returns nothing:
def plusTen(i: Int) { println(i+10) }
When you pass plusTen into runAFunction, you’ll see that it also works, printing 52:
runAFunction(plusTen) // prints 52
Although these examples don’t do too much yet, you can see the power of HOFs:
You can easily swap in interchangeable algorithms.
As long as the signature of the function you pass in matches the signature that’s expected, your algorithms can do anything you want. This is comparable to swapping out algorithms in the OOP Strategy design pattern.
Let’s keep building on this…
Here’s a function named executeNTimes that has two input parameters: a function, and an Int:
def executeNTimes(f: () => Unit, n: Int) {
for (i <- 1 to n) f()
}
As the code shows, executeNTimes executes the f function n times. To test this, define a function that matches f’s signature:
def helloWorld(): Unit = { println("Hello, world") }
and then pass this function into executeNTimes along with an Int:
scala> executeNTimes(helloWorld, 3)
Hello, world
Hello, world
Hello, world
As expected, executeNTimes executes the helloWorld function three times. Cool.
Next, here’s a function named executeAndPrint that takes a function and two Int parameters, and returns nothing. It defines the FIP f as a function that takes two Int values and returns an Int:
def executeAndPrint(f: (Int, Int) => Int, x: Int, y: Int): Unit = {
val result = f(x, y)
println(result)
}
executeAndPrint passes the two Int parameters it’s given into the FIP it’s given in this line of code:
val result = f(x, y)
Except for the fact that this function doesn’t have a return value, this example shows a common FP technique:
Your function takes a FIP.
It takes other parameters that work with that FIP.
You apply the FIP (
f) to the parameters as needed, and return a value. (Or, in this example of a function with a side effect, you print something.)
To demonstrate executeAndPrint, let’s create some functions that match f’s signature. Here are a couple of functions take two Int parameters and return an Int:
def sum(x: Int, y: Int) = x + y
def multiply(x: Int, y: Int) = x * y
Now you can call executeAndPrint with these functions as the first parameter and whatever Int values you want to supply as the second and third parameters:
executeAndPrint(sum, 3, 11) // prints 14
executeAndPrint(multiply, 3, 9) // prints 27
Let’s keep building on this…
Now let’s define a function that takes multiple FIPs, and other parameters to feed those FIPs. Let’s define a function like this:
It takes one function parameter that expects two
Ints, and returns anIntIt takes a second function parameter with the same signature
It takes two other
IntparametersThe
Ints will be passed to the two FIPsIt will return the results from the first two functions as a tuple — a
Tuple2, to be specific
Since I learned FP, I like to think in terms of “Function signatures first,” so here’s a function signature that matches those bullet points:
def execTwoFunctions(f1:(Int, Int) => Int,
f2:(Int, Int) => Int,
a: Int,
b: Int): Tuple2[Int, Int] = ???
Given that signature, can you imagine what the function body looks like?
(I’ll pause for a moment to let you think about that.)
Here’s what the complete function looks like:
def execTwoFunctions(f1: (Int, Int) => Int,
f2: (Int, Int) => Int,
a: Int,
b: Int): Tuple2[Int, Int] = {
val result1 = f1(a, b)
val result2 = f2(a, b)
(result1, result2)
}
That’s a verbose (clear) solution to the problem. You can shorten that three-line function body to just this, if you prefer:
(f1(a,b), f2(a,b))
Now you can test this new function with the trusty sum and multiply functions:
def sum(x: Int, y: Int) = x + y
def multiply(x: Int, y: Int) = x * y
Using these functions as input parameters, you can test execTwoFunctions:
val results = execTwoFunctions(sum, multiply, 2, 10)
The REPL shows the results:
scala> val results = execTwoFunctions(sum, multiply, 2, 10)
results: (Int, Int) = (12,20)
I hope this gives you a taste for not only how to write HOFs, but the power of using them in your own code.
Okay, that’s enough examples for now. I’ll cover two more topics before finishing this lesson, and then in the next lesson you can see how to write a map function with everything I’ve shown so far.
A nice thing about Scala is that once you know how things work, you can see the consistency of the language. For example, the syntax that you use to define FIPs is the same as the “explicit return type” (ERT) syntax that you use to define functions.
I show the ERT syntax in detail in the “Explaining Scala’s
valFunction Syntax” appendix.
What I mean by this is that earlier I defined this function:
sampleFunction(f: (Int, Int) => Int)
The part of this code that defines the FIP signature is exactly the same as the ERT signature for the sum function that I define in the val Function Syntax appendix:
val sum: (Int, Int) => Int = (a, b) => a + b
You can see what I mean if you line the two functions up, as shown in Figure [fig:fipSigSameAsSumErt].

Once you understand the FIP type signature syntax, it becomes easier to read things like the ERT function syntax and the Scaladoc for HOFs.
Personally, I’m rarely smart enough to see exactly what I want to do with all of my code beforehand. Usually I think I know what I want to do, and then as I start coding I realize that I really want something else. As a result of this, my usual thought process when it comes to writing HOFs looks like this:
I write some code
I write more code
I realize that I’m starting to duplicate code
Knowing that duplicating code is bad, I start to refactor the code
Actually, I have this same thought process whether I’m writing OOP code or FP code, but the difference is in what I do next.
With OOP, what I might do at this point is to start creating class hierarchies. For instance, if I was working on some sort of tax calculator in the United States, I might create a class hierarchy like this:
trait StateTaxCalculator
class AlabamaStateTaxCalculator extends StateTaxCalculator ...
class AlaskaStateTaxCalculator extends StateTaxCalculator ...
class ArizonaStateTaxCalculator extends StateTaxCalculator ...
Conversely, in FP, my approach is to first define an HOF like this:
def calculateStateTax(f: Double => Double, personsIncome: Double): Double = ...
Then I define a series of functions I can pass into that HOF, like this:
def calculateAlabamaStateTax(income: Double): Double = ...
def calculateAlaskaStateTax(income: Double): Double = ...
def calculateArizonaStateTax(income: Double): Double = ...
As you can see, that’s a pretty different thought process.
Note: I have no idea whether I’d approach these problems exactly as shown. I just want to demonstrate the difference in the general thought process between the two approaches, and in that regard — creating a class hierarchy versus a series of functions with a main HOF — I think this example shows that.
To summarize this, the thought process, “I need to refactor this code to keep it DRY,” is the same in both OOP and FP, but the way you refactor the code is very different.
A function that takes another function as an input parameter is called a “Higher Order Function,” or HOF. This lesson showed how to write HOFs in Scala, including showing the syntax for function input parameters (FIPs) and how to execute a function that is received as an input parameter.
As the lesson showed, the general syntax for defining a function as an input parameter is:
variableName: (parameterTypes ...) => returnType
Here are some examples of the syntax for FIPs that have different types and numbers of arguments:
def exec(f:() => Unit) = ??? // note: i don't show the function body
// for any of these examples
def exec(f: String => Int) // parentheses not needed
def exec(f: (String) => Int)
def exec(f: (Int) => Int)
def exec(f: (Double) => Double)
def exec(f: (Person) => String)
def exec(f: (Int) => Int, a: Int, b: Int)
def exec(f: (Pizza, Order) => Double)
def exec(f: (Pizza, Order, Customer, Discounts) => Currency)
def exec(f1: (Int) => Int, f2:(Double) => Unit, s: String)
In this lesson I showed how to write HOFs. In the next lesson we’ll put this knowledge to work by writing a complete map function that uses the techniques shown in this lesson.