Functional Programming is Like Unix Pipelines
The primary goal of this lesson is to show that you can think of writing functional programs as being like writing Unix pipeline commands. Stated another way, if you’ve written Unix pipeline commands before, you have probably written code in a functional style, whether you knew it or not.
As a second, smaller goal, I want to demonstrate a few ways that you can look at your code visually to help you “Think in FP.”
Note: This section is written for Unix and Linux users. If you don’t know Unix, (a) I highly recommend learning it, and (b) you may want to (sadly) skip this section, as it may not make much sense unless you know the Unix commands that I show.
One way to think about FP is that it’s like writing Unix/Linux pipeline commands, i.e., a series of two or more commands that you combine at the Unix command line to get a desired result.
For example, imagine that your boss comes to you and says, “I need a script that will tell me how many unique users are logged into a Unix system at any given time.” How would you solve this problem?
Knowing Unix, you know that the who command shows the users that are currently logged in. So you know that you want to start with who — that’s your data source. To make things interesting, let’s assume that who doesn’t support any command-line arguments, so all you can do is run who without arguments to generate a list of users logged into your system, like this:
$ who
al console Oct 10 10:01
joe ttys000 Oct 10 10:44
tallman ttys001 Oct 10 11:05
joe ttys002 Oct 10 11:47
who’s output is well structured and consistent. It shows the username in the first column, the “console” they’re logged in on in the second column, and the date and time they logged in on in the last columns.
Some Unix systems may show the IP address the user is logged in from. I left that column off of these examples to keep things simple.
If you didn’t have to automate this solution, you could solve the problem by looking at the unique usernames in the first column. In this case there are four lines of output, but only three of the usernames are unique — al, joe, and tallman — so the current answer to your boss’s question is that there are three unique users logged into the system at the moment.
Now that you know how to solve the problem manually, the question becomes, how do you automate this solution?
The solution’s algorithm appears to be:
Run the
whocommandCreate a list of usernames from the first column
Get only the unique usernames from that list
Count the size of that list
In Unix that algorithm translates to chaining these commands together:
Start with
whoas the data sourceUse a command like
cutto create the list of usernamesUse
uniqto get only the unique usernames from that listUse
wc -lto count those unique usernames
A good solution for the first two steps is to create this simple Unix pipeline:
who | cut -d' ' -f1
That cut command can be read as, “Using a blank space as the field separator (-d), print the first field (-f1) of every row of the data stream from STDIN to STDOUT.” That pipeline command results in this output:
al
joe
tallman
joe
Notice what I did here: I combined two Unix commands to get a desired result. If you think of the who command as providing a list of strings, you can think of the cut command as being a pure function: it takes a list of strings as an input parameter, runs a transformation algorithm on that incoming data, and produces an output list of strings. It doesn’t use anything but the incoming data and its algorithm to produce its result.
As a quick aside, the signature for a Scala cut function that works like the Unix cut command might be written like this:
def cut(strings: Seq[String],
delimiter: String,
field: Int): Seq[String] = ???
Getting back to the problem at hand, my current pipeline command generates this output:
al
joe
tallman
joe
and I need to transform that data into a “number of unique users.”
To finish solving the problem, all I need to do is to keep combining more pure functions — er, Unix commands — to get the desired answer. That is, I need to keep transforming the data to get it into the format I want.
The next thing I need to do is reduce that list of all users down to a list of unique users. I do that by adding the uniq command to the end of the current pipeline:
who | cut -d' ' -f1 | uniq
uniq transforms its STDIN to this STDOUT:
al
joe
tallman
Now all I have to do to get the number of unique users is count the number of lines that are in the stream with wc -l:
who | cut -d' ' -f1 | uniq | wc -l
That produces this output:
3
Whoops. What’s that 3 doing way over there to the right? I want to think of my result as being an Int value, but this is more like a String with a bunch of leading spaces. What to do?
Well, it’s Unix, so all I have to do is add another command to the pipeline to transform this string-ish result to something that works more like an integer.
There are many ways to handle this, but I know that the Unix tr command is a nice way to remove blank spaces, so I add it to the end of the current pipeline:
who | cut -d' ' -f1 | uniq | wc -l | tr -d ' '
That gives me the final, desired answer:
3
That looks more like an integer, and it won’t cause any problem if I want to use this result as an input to some other command that expects an integer value (with no leading blank spaces).
If you’ve never used the
trcommand before, it stands for translate, and I wrote a fewtrcommand examples many years ago.
Now that I have a solution as a Unix pipeline, I can convert it into a little shell script. For the purposes of this lesson, I’ll write it in a verbose manner rather than as a pipeline:
WHO=`who`
RES1=`echo $WHO | cut -d' ' -f1`
RES2=`echo $RES1 | uniq`
RES3=`echo $RES2 | wc -l`
RES4=`echo $RES3 | tr -d ' '`
echo $RES4
Hmm, that looks suspiciously like a series of expressions, followed by a print statement, doesn’t it? Some equivalent Scala code might look like this:
val who: Seq[String] = getUsers // an impure function
val res1 = cut(who, " ", 1)
val res2 = uniq(res1)
val res3 = countLines(res2)
val res4 = trim(res3)
println(res4) // a statement
I usually write “one expression at a time” code like this when I first start solving a problem, and eventually see that I can combine the expressions. For example, because the first and last lines of code are impure functions I might want to leave them alone, but what about these remaining lines:
val res1 = cut(who, " ", 1)
val res2 = uniq(res1)
val res3 = countLines(res2)
val res4 = trim(res3)
In the first line, because cut is a pure function, res1 and cut(who, , 1) will always be equivalent, so I can eliminate res1 as an intermediate value:
val res2 = uniq(cut(who, " ", 1))
val res3 = countLines(res2)
val res4 = trim(res3)
Next, because res2 is always equivalent to the right side of its expression, I can eliminate res2 as an intermediate value:
val res3 = countLines(uniq(cut(who, " ", 1)))
val res4 = trim(res3)
Then I eliminate res3 for the same reason:
val res4 = trim(countLines(uniq(cut(who, " ", 1))))
Because there are no more intermediate values, it makes sense to rename res4:
val result = trim(countLines(uniq(cut(who, " ", 1))))
If you want, you can write the entire original series of expressions and statements — including getUsers and the println statement — like this:
println(trim(countLines(uniq(cut(getUsers, " ", 1)))))
As a recap, I started with this:
val who: Seq[String] = getUsers
val res1 = cut(who, " ", 1)
val res2 = uniq(res1)
val res3 = countLines(res2)
val res4 = trim(res3)
println(res4)
and ended up with this:
println(trim(countLines(uniq(cut(getUsers, " ", 1)))))
The thing that enables this transformation is that all of those expressions in the middle of the original code are pure function calls.
This is the Scala equivalent of the Unix pipeline solution:
who | cut -d' ' -f1 | uniq | wc -l | tr -d ' '
I always find solutions like this amusing, because if you have ever seen Lisp code, condensed Scala/FP code tends to look like this, where you read the solution starting at the inside (with
getUsers), and work your way out (tocut, thenuniq, etc.).
Note: You don’t have to use this condensed style. Use whatever you’re comfortable with.
“That’s great,” you say, “but how is this like functional programming?”
Well, if you think of the who command as generating a list of strings (Seq[String]), you can then think of cut, uniq, wc, and tr as being a series of transformer functions, because they transform the input they’re given into a different type of output, as shown in Figure [fig:unixPipelines1].
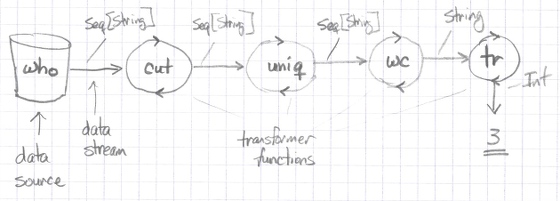
Looking at just the wc command — and thinking of it as a pure function — you can think of it as taking a Seq[String] as its first input parameter, and when it’s given the -l argument, it returns the number of lines that it counts in that Seq.
In these ways the wc command is a pure function:
It takes a
Seq[String]as inputIt does not rely on any other state or hidden values
It does not read or write to any files
It does not alter the state of anything else in the universe
Its output depends only on its input
Given the same input at various points in time, it always returns the same value
The one thing that wc did that I didn’t like is that it left-pads its output with blank spaces, so I used the tr command just like the wc command to fix that problem: as a pure function.
A nice way to think of this code is like this:
Input -> Transformer -> Transformer ... Transformer-> Output
With that thought, this example looks as shown in Figure [fig:unixPipelines2].
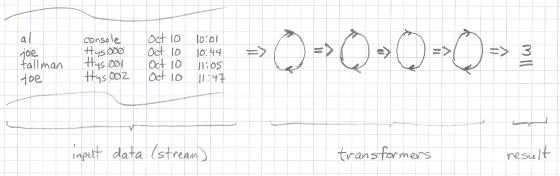
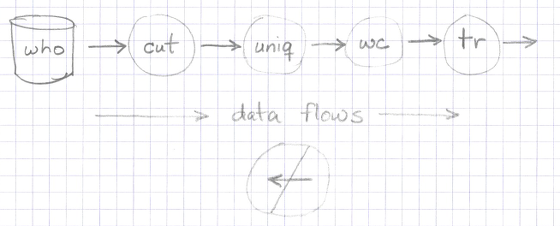
Note a few key properties in all of this. First, data flows in only one direction, as shown in Figure [fig:unixPipelinesDataFlow].
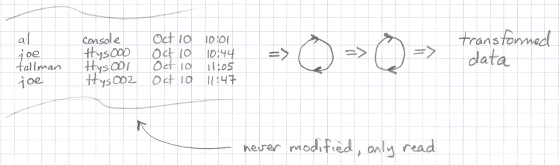
Second, Figure [fig:unixPipelineDataNotModified] shows that the input data a function is given is never modified.
Finally, as shown in Figure [fig:unixFunctionsEntranceExit], you can think of functions as having an entrance and an exit, but there are no side doors or windows for data to slip in or out.
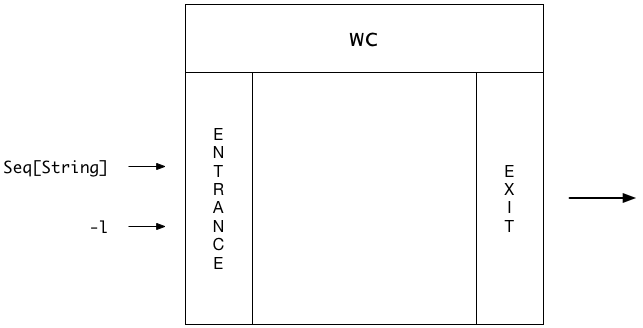
These are all important properties of pure functions (and Unix commands).
There’s another interesting point about this example in regards to FP. When I combine these commands together like this:
who | cut -d' ' -f1 | uniq | wc -l | tr -d ' '
I create what’s called in Unix a pipeline or command pipeline. In FP we call that same thing a combinator. That is, I combined the three commands — pure functions — together to get the data I wanted.
If I had structured my Scala code differently I could have made it look like this:
who.cut(delimiter=" ", field=1)
.uniq
.wc(lines = true)
.tr(find=" ", replace="")
I’ll add a more formal definition of “combinator” later in this book, but in general, when you see code like this — a chain of functions applied to some initial data — this is what most people think when they use the term “combinator.” This is another case where an FP term sounds scary, but remember that whenever you hear the term “combinator” you can think “Unix pipeline.”
At this point it’s worth taking a moment to think about the thought process involved in solving this problem. If you look back at how it was solved, our thinking followed these steps:
We started with the problem statement: wanting to know how many users are logged into the system.
We thought about what data source had the information we needed, in this case the output of the
whocommand.At this point should note that implicit in my own thinking is that I knew the structure of the data I’d get from the
whocommand. That is, as an experienced Unix user I knew thatwhoreturns a list of users, with each user login session printed on a new line.Depending on your thought process you may have thought of the
whooutput as a multilineStringor as aList(or more generally as aSeqin Scala). Either thought is fine.Because you knew the structure of the
whodata, and you know your Unix commands, you knew that you could apply a sequence of standard commands to thewhodata to get the number of unique users.You may or may not have known beforehand that the
wc -loutput is padded with blank spaces. I did not.
The reason I mention this thought process is because that’s what the functional programming thought process is like:
You start with a problem to solve.
You either know where the data source is, or you figure it out.
Likewise, the data is either in a known format, or in a format you need to learn.
You clearly define the output you want in the problem statement.
You apply a series of pure functions to the input data source(s) to transform the data into a new structure.
If all of the functions that you need already exist, you use them; otherwise you write new pure functions to transform the data as needed.
Note the use of the word apply in this discussion. Functional programmers like to say that they apply functions to input data to get a desired output. As you saw, using the word “apply” in the previous discussion was quite natural.
As a second example of both “Unix pipelines as FP,” and “The FP thought process,” imagine that you want a sorted list of all users who are currently logged in. How would you get the desired answer?
Let’s follow that thought process again. I’ll give you the problem statement, and everything after that is up to you.
Problem statement: I want a sorted list of all users who are currently logged in.
The data source is:
The data format looks like this:
The desired output format is:
The command pipeline needed to get the output data from the input data is:
Do you need to create any new functions to solve this problem? If so, define them here:
Here’s my solution:
who | cut -f1 -d' ' | uniq | sort
That exercise was intentionally a relatively simple variation of the original exercise. Here are a few more advanced exercises you can work to get the hang of this sort of problem solving:
Write a pipeline to show the number of processes owned by the root user.
Write a pipeline to show the number of open network connections. (Tip: I use
netstatas the data source.)Use the
lsofcommand to show what computers your computer is currently connected to.Write a pipeline command to show which processes are consuming the most RAM on your computer.
Write a command to find the most recent .gitignore file on your computer.
Besides demonstrating how writing Unix pipeline commands are like writing FP code (and vice-versa), I’m also trying to demonstrate “The FP Thought Process.” Because “output depends only on input,” FP lends itself to something that used to be called “Data Flow Diagrams” — or DFDs — back in the old days.
There’s a formal notation for DFDs, but I don’t care for it. (There are actually several formal notations.) If I was going to sketch out the solution to the last problem, I’d draw it like the image in Figure [fig:unixDfdSketch].
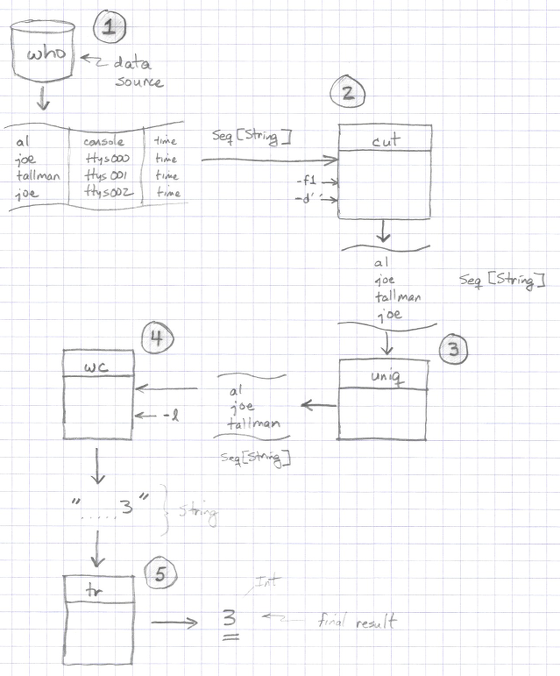
Because I’m using my own graphical drawing language here, I’ll note that at the moment:
I prefer to draw data flows as streams (simple tables).
I like to annotate streams with their data types.
I like to draw functions as rectangles (because of the whole front-door/back-door, entrance/exit concept).
I’m not suggesting that you have to draw out every problem and solution like this, but if you’re working on a hard problem, this can be helpful.
If I’m working on a difficutl problem, or trying to explain a solution to other people, I like to draw visual diagrams like that. The book, Complete Systems Analysis, by Robertson and Robertson, defines something else that they call a “Rule of Data Conservation,” which they state like this:
“Each process (function) in the data flow diagram must be able to produce the output data flows from its input.”
Using their diagramming process, the data that flows from the who command would be described like this:
Who = Username + Terminal + Date + Time
If you take the time to draw the data flows like this, it’s possible to make sure that the “Rule of Data Conservation” is satisfied — at least assuming that you know each function’s algorithm.
A set of Power Point slides at DePaul.edu (that is hard to link to because of the whole “PPT” thing) makes the following observations about data flows:
Data stays at rest unless moved by a process
Processes cannot consume or create data
Must have at least 1 input data flow (to avoid miracles)
Must have at least 1 output data flow (to avoid black holes)
Just substitute “function” for “process” in their statements, and I really like those last two lines — avoiding black holes and miracles — as they apply to writing pure functions.
In this lesson I tried to show how writing Unix pipeline commands is like writing FP code. This is true in that combining Unix commands to solve a problem is like combining pure functions to solve a problem.
One part I didn’t show is a program that runs continuously until the user selects a “Quit” option. But fear not, I will show this in an upcoming lesson, I just need to provide a little more background information, including covering topics like recursive programming.
As I mentioned at the beginning, my main goal for this lesson is to demonstrate that writing Unix pipeline commands is like writing functional code. Just like functional programming, when you write Unix pipeline commands:
You have data sources, or inputs, that bring external data into your application.
Unix commands such as
cut,uniq, etc., are like pure functions. They take in immutable inputs, and generate output based only on those inputs and their algorithms.You combine Unix commands with pipelines in the same way that you use FP functions as “combinators.”